Artificial intelligence

Particle Swarm optimization (PSO) in 1995 Eberhart and Dr. It is an intuitive optimization technique developed by Kennedy based on Population. It has been developed by inspiration from the social behavior of the kuş or fish herds.

PSO shows many similarities with evolutionary computing techniques, such as genetic algorithms. The system starts with a population of random solutions and searches for the best solution by updating generations. In contrast to this, unlike GA, there are no evolutionary operators, such as intersecting and mutation, in PSO. Potential solutions, known as particles in PSO, travel in problem space by following the best available solutions(they fly).

If it is compared with GA, the advantage of PSO is that it is easy to perform and has very few parameters to adjust. PSO has been successfully applied in many areas. Some of these include function optimization, artificial neural networks training, fuzzy System Control, and other areas where GA can be applied.

There are many computational techniques inspired by biological systems. For example, artificial neural networks are a simplified model of the human brain. Genetic algorithms are inspired by the evolutionary process in biology. Here, the subject discussed is a different type of biological systems, social systems. In particular, the Association behaviors of simple individuals who interact with each other and with their environment are examined. This concept is called particle Intelligence.

ALGORITHM

As explained earlier, the PSO simulates the behavior of the kuş or the flock of fish. Let us assume that there is a group of birds looking for random food in one area and there is only one piece of food in the searched area. None of the birds know where to eat. But at the end of each iteration, let them know how far away the food is. What is the best strategy in this case? The most effective is to follow the person closest to the food.

PSO works in this scenario and is used to solve optimization problems. In PSO, each solution is a quitter in search space, and they are called a “particle”. All particles have speed information that directs a compatibility value and flight as assessed by the fitness function to be optimized. Particles fly by following the optimum particles present in problem space.

The PSO is started with a set of randomised solutions (particles) and the generation is updated to look for the most appropriate value. In each iteration, each particle is updated according to two “best” values. The first one is the best compatibility value that a particle has ever found. In addition, this value is stored in memory for later use and is called “pbest”, which is the best value of the particle. The other best value is the solution that has the best compatibility value ever obtained by any particle in the population. This value is the global best value for the population and is called “gest”.

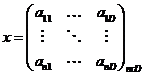
For a particle, the population matrix is expressed as follows: According to the matrix, i. the particle is shown in the form. the second particle is expressed as the velocity vector, which shows the amount of change in each

position. After these two best values are found, they update the particle, speed and

position according to the following equations (1) and (2):

 

 

PSO PARAMETERS

One of the advantages of PSO is that it works with real numbers. As with genetic algorithms, there is no need for operators to convert from binary coding or to use some special algorithms. For example, let’s try to find the solution for the function. Since there are 3 unknown, D=3 is dimensioned and is set in the form of particles. the function is also used as a fitness function. The standard procedure given above is then applied to find the optimality. Maximum number of iterations or minimum error conditions are used as the end criteria. As seen, there are very few parameters needed in the PSO. The list of these parameters and their typical values are given below.

The number of particles is usually between 20 and 40. In fact, for most problems, 10 is sufficient to achieve good solutions. For some difficult or special problems, it may be necessary to use 100 or 200 particles.

The particle size varies according to the problem to be optimized.

Particle spacing varies according to the problem to be optimized, but particles can be defined in different sizes and ranges.

Vmax: determines the maximum change (speed) that will occur in a particle in an iteration. Usually determined by particle spacing. For example, if the x1 particle (-10.10) is in range, Vmax=20 can be irritated.

Learning factors: C1 and C2 are usually chosen as 2. But it can be chosen differently. Usually C1 equals C2 and [0, 4] is selected.

Stop condition: the algorithm can be stopped when the maximum number of iterations is reached or when the value function reaches the desired level.

NUMERICAL SOLUTION EXAMPLE

In this section, we will examine the calculations through a sample so that the working logic of the PSO algorithm can be understood in a more concrete way. For this purpose, the test function, known as “six-hump camel-back (six-kamburlu camel-back)”, is considered in the literature. The problem is named this way because it has a total of 6 local minimums, two of which are global minimum.